HIGH PASS FILTERS BASIC INFORMATION AND TUTORIALS

Swapping the cap and the resistor in the low-pass circuit creates another type of circuit called a high-pass filter. Using your now supreme powers of deduction and intuition, you are thinking to yourself, “I’ll bet that means the circuit passes high frequencies while blocking low ones.

 ” You are correct, and the circuit looks like the one in Figure 2.34 .Hopefully, after our discussion on the low-pass circuit, the operation of this one is clear.

The cap acts like a larger resistor at low frequencies, making the voltage divider knock down the output. At higher frequencies the cap passes more current as it becomes a short, causing a higher voltage at the output.

The inductor version of this circuit looks like Figure 2.35

As you might have suspected, this fi lter is the inverse, circuit-wise, of the RC high-pass filter. Another little bit of serendipity is the fact that the half-voltage output point 29 is also at 1/tau ( tau means time constant generically, whether referring to an RC or an RL circuit), just like the low-pass filters.

To sum up, the high-pass and low-pass fi lters take advantage of the frequency response of either a capacitor or an inductor. This is done by combining them with a resistor to create a voltage divider that attenuates the unwanted frequencies while allowing the desired ones to pass.

Some cool things happen when we put the two reactive elements together. You can create notch and band pass filters where a specifi c band of frequencies is knocked out, or a specific band is passed while all others are blocked.

The phenomenon of resonance also occurs in what is called a tank circuit, where you have a capacitor combined with an inductor. The tank circuit will oscillate current back and forth from one component to the other.

LOW PASS FILTERS BASIC INFORMATION AND TUTORIALS

WHAT ARE LOW PASS FILTERS?

Consider the circuit shown in Figure 2.32 . Note similarities to the RC circuit that we used to first understand the effects of a capacitor. The difference is that now we are going to apply an AC signal to the input rather than the step input we applied before.

This circuit is known as a low-pass fi lter, and all you really need to know to understand it is the voltage divider rule and how a capacitor reacts to frequency. If this were a simple voltage divider, you could figure out, based on the ratio of the resistors, how much voltage would appear at the output.

Remember that the cap is like a resistor that depends on frequency and try to extrapolate what will happen as frequency sweeps from zero to infinity. At low frequencies the cap doesn’t pass much current, so the signal isn’t affected much.

As frequency increases, the cap will pass more and more current, shorting the output of the resistor to ground and dividing the output voltage to smaller and smaller levels. There is a magic point at which the output is half the input.

It is when the frequency equals 1/RC. You might have noticed that this is the inverse of the time constant that we used earlier when we first looked at caps. Kinda cool when it all comes together, isn’t it? This is known as a low-pass filter because it passes low frequencies while reducing or attenuating high frequencies. You can make a low-pass filter with an inductor and resistor, too.

Given that the inductor behaves in a way that is opposite of a capacitor, can you imagine what that might look like? Have a look at Figure 2.33 .

That’s right; you swap the position of the components. That’s because the inductor (being the opposite of a cap) passes the lower frequencies and blocks the higher frequencies. It performs the same function as the low-pass RC circuit but in a slightly different manner. You still have a voltage-divider circuit, but instead of the resistor-to-ground changing, the input resistor is changing.

At low frequencies the inductor is a short, making the ground resistor of little effect. As frequencies increase, the inductor chokes 28 off the current, reacting in a way that makes the input element of the voltage divider seem like an increasingly large resistance.

This in turn makes the resistor to ground have a much bigger say in the ratio of the voltage-divider circuit. To summarize, in the low-pass fi lter circuits, as the frequencies sweep from low to high, the cap starts out as an open and moves to a short while the inductor starts out as a short and becomes an open.

By positioning these components in opposite locations in the voltage-divider circuit, you create the same filtering effect. The ratio of the voltage divider in both types of fi lters decreases the output voltage as frequencies increase.

All this lets the low frequencies pass and blocks the high frequencies. Now, what do you suspect might happen if we swap the position of the components in these circuits?

STATIC COMPENSATOR (STATCOM) DEFINITION BASIC AND TUTORIALS

This is a shunt device that does not require passive elements like inductors and capacitors. The schematic diagram of a SMIB power system that is compensated by a shunt compensator is shown in Figure 1.10. The STATCOM is built around a voltage source inverter, which is supplied by a dc capacitor. The inverter consists of GTO switches which are turned on and off through a gate drive circuit.

The output of the voltage source inverter is connected to that ac system through a coupling transformer. The inverter produces a quasi sinewave voltage Vo at the fundamental frequency. Let us assume that the losses in the inverter and the coupling transformer are negligible.

The inverter is then gated such that the output voltage of the inverter Vo is in phase with the local bus voltage v. In this situation two ac voltages that are in phase are connected together through a reactor, which is the leakage reactance of the coupling transformer.

Therefore the current ['I is a purely reactive. If the magnitude of the voltage Vm is more than that of the voltage Vo, the reactive current Iq flows from the bus to the inverter. Then the inverter will consume reactive power.

If, on the other hand, the magnitude of Vo is greater than that of Vm, then the inverter feeds reactive power to the system. Therefore through this arrangement the STATCOM can generate or absorb reactive power.

In practice how ever the losses are not negligible and must be drawn from the ac system. This is accomplished by slightly shifting the phase angle of the voltage Vo through a feedback mechanism such that the de capacitor voltage is held constant.

The structure of the GTO-based VSI must be so chosen that the lower order harmonics are eliminated from the output voltage. The VSI will then resemble a synchronous voltage source. Because the switching frequency of each GTOs must be kept low, overall switch ripple needs to be kept low without use of PWM.

This is accomplished by connecting a large number of basic inverter modules. The construction of a 48-step voltage source inverter is discussed in [19].

In this inverter, eight identical elementary 6-step inverters are operated from a common dc bus. Each of these 6-step inverters produces a compatible set of three-phase, quasi-square wave output voltage waveforms.

The outputs of these 6-step inverters are added through a magnetic circuit that contains eighteen single phase three winding transformers and six single-phase two winding transformers. This connection eliminates all low-order harmonics.

The lowest order harmonic on the ac side is 47th while that on the dc side is 48th . The line-to-line output\ voltage of the 48-step inverter is shown in Figure 1.11 along with the fundamental voltage. It can be seen that the output is a stepped approximation of the fundamental sinewave. The construction of a multilevel synchronous voltage source is given in.

VARIABLE RESISTORS DEFINITION BASIC AND TUTORIALS

Potentiometers. The potentiometer is a special form of variable resistor with three terminals. Two terminals are connected to the opposite sides of the resistive element, and the third connects to a sliding contact that can be adjusted as a voltage divider.

Potentiometers are usually circular in form with the movable contact attached to a shaft that rotates. Potentiometers are manufactured as carbon composition, metallic film, and wire-wound resistors available in single-turn or multiturn units.

The movable contact does not go all the way toward the end of the resistive element, and a small resistance called the hop-off resistance is present to prevent accidental burning of the resistive element.

Rheostat. The rheostat is a current-setting device in which one terminal is connected to the resistive element and the second terminal is connected to a movable contact to place a selected section of the resistive element into the circuit.

Typically, rheostats are wire-wound resistors used as speed controls for motors, ovens, and heater controls and in applications where adjustments on the voltage and current levels are required, such as voltage dividers and bleeder circuits.

FIXED RESISTORS DEFINITION BASIC AND TUTORIALS

The fixed resistors are those whose value cannot be varied after manufacture. Fixed resistors are classified into composition resistors, wire-wound resistors, and metal-film resistors. Table 1.2 outlines the characteristics of some typical fixed resistors.


TABLE 1.2 Characteristics of Typical Fixed Resistors
Operating
Resistor Types Resistance Range Watt Range Temp. Range a, ppm/°C
Wire-wound resistor
Precision 0.1 to 1.2 MW 1/8 to 1/4 –55 to 145 10
Power 0.1 to 180 kW 1 to 210 –55 to 275 260
Metal-film resistor
Precision 1 to 250 MW 1/20 to 1 –55 to 125 50–100
Power 5 to 100 kW 1 to 5 –55 to 155 20–100
Composition resistor
General purpose 2.7 to 100 MW 1/8 to 2 –55 to 130 1500



Wire-Wound Resistors. Wire-wound resistors are made by winding wire of nickel-chromium alloy on a ceramic tube covering with a vitreous coating. The spiral winding has inductive and capacitive characteristics that make it unsuitable for operation above 50 kHz. The frequency limit can be raised by noninductive winding so that the magnetic fields produced by the two parts of the winding cancel.

Composition Resistors. Composition resistors are composed of carbon particles mixed with a binder. This mixture is molded into a cylindrical shape and hardened by baking.

Leads are attached axially to each end, and the assembly is encapsulated in a protective encapsulation coating. Color bands on the outer surface indicate the resistance value and tolerance. Composition resistors are economical and exhibit low noise levels for resistances above 1 MW.

Composition resistors are usually rated for temperatures in the neighborhood of 70°C for power ranging from 1/8 to 2 W. Composition resistors have end-to-end shunted capacitance that may be noticed at frequencies in the neighborhood of 100 kHz, especially for resistance values above 0.3 MW.

Metal-Film Resistors. Metal-film resistors are commonly made of nichrome, tin-oxide, or tantalum nitride, either hermetically sealed or using molded-phenolic cases. Metal-film resistors are not as stable as the wire wound resistors.

Depending on the application, fixed resistors are manufactured as precision resistors, semiprecision resistors, standard general-purpose resistors, or power resistors. Precision resistors have low voltage and power coefficients, excellent temperature and time stabilities, low noise, and very low reactance.

These resistors are available in metal-film or wire constructions and are typically designed for circuits having very close resistance tolerances on values. Semiprecision resistors are smaller than precision resistors and are primarily used for current-limiting or voltage-dropping functions in circuit applications. Semiprecision resistors have long-term temperature stability.

General-purpose resistors are used in circuits that do not require tight resistance tolerances or long-term stability. For general-purpose resistors, initial resistance variation may be in the neighborhood of 5% and the variation in resistance under full-rated power may approach 20%.

Typically, general-purpose resistors have a high coefficient of resistance and high noise levels. Power resistors are used for power supplies, control circuits, and voltage dividers where operational stability of 5% is acceptable. Power resistors are available in wire-wound and film constructions. Film-type power resistors have the advantage of stability at high frequencies and have higher resistance values than wire-wound resistors for a given size.

ELECTRIC CHARGE BASIC DEFINITION INFORMATION AND TUTORIALS

WHAT IS AN ELECTRIC CHARGE?


It was a major scientific accomplishment to integrate an understanding of electricity with fundamental concepts about the microscopic nature of matter. Observations of static electricity like those mentioned earlier were elegantly explained by Benjamin Franklin in the late 1700s as follows: There exist in nature two types of a property called charge, arbitrarily labeled “positive” and “negative.”

Opposite charges attract each other, while like charges repel. When certain materials rub together, one type of charge can be transferred by friction and “charge up” objects that subsequently repel objects of the same kind (hair), or attract objects of a different kind (polyester and cotton, for instance).

Through a host of ingenious experiments, scientists arrived at a model of the atom as being composed of smaller individual particles with opposite charges, held together by their electrical attraction. Specifically, the nucleus of an atom, which constitutes the vast majority of its mass, contains protons with a positive charge, and is enshrouded by electrons with a negative charge.

The nucleus also contains neutrons, which resemble protons, except they have no charge. The electric attraction between protons and electrons just balances the electrons’ natural tendency to escape, which results from both their rapid movement, or kinetic energy, and their mutual electric repulsion. (The repulsion among protons in the nucleus is overcome by another type of force called the strong nuclear interaction, which only acts over very short distances.)

This model explains both why most materials exhibit no obvious electrical properties, and how they can become “charged” under certain circumstances: The opposite charges carried by electrons and protons are equivalent in magnitude, and when electrons and protons are present in equal numbers (as they are in a normal atom), these charges “cancel” each other in terms of their effect on their environment. Thus,
from the outside, the entire atom appears as if it had no charge whatsoever; it is electrically neutral.

Yet individual electrons can sometimes escape from their atoms and travel elsewhere. Friction, for instance, can cause electrons to be transferred from one material into another. As a result, the material with excess electrons becomes negatively charged, and the material with a deficit of electrons becomes positively charged (since the positive charge of its protons is no longer compensated). The ability of electrons to travel also explains the phenomenon of electric current, as we will see shortly.

Some atoms or groups of atoms (molecules) naturally occur with a net charge because they contain an imbalanced number of protons and electrons; they are called ions. The propensity of an atom or molecule to become an ion—namely, to release electrons or accept additional ones—results from peculiarities in the geometric pattern by which electrons occupy the space around the nuclei.

Even electrically neutral molecules can have a local appearance of charge that results from imbalances in the spatial distribution of electrons—that is, electrons favoring one side over the other side of the molecule. These electrical phenomena within molecules determine most of the physical and chemical properties of all the substances we know.

While on the microscopic level, one deals with fundamental units of charge (that of a single electron or proton), the practical unit of charge in the context of electric power is the coulomb (C). One coulomb corresponds to the charge of 6.25 x 10^18 protons. Stated the other way around, one proton has a charge of 1.6 x 10^-19 C. One electron has a negative charge of the same magnitude, -1.6 10^-19 C. In equations, charge is conventionally denoted by the symbol Q or q.

THE OHM'S LAW BASIC DEFINITION INFORMATION AND TUTORIALS

WHAT IS OHM'S LAW?


It is intuitive that voltage and current would be somehow related. For example, if the potential difference between two ends of a wire is increased, we would expect a greater current to flow, just like the flow rate of gas through a pipeline increases when a greater pressure difference is applied.

For most materials, including metallic conductors, this relationship between voltage and current is linear: as the potential difference between the two ends of the conductor increases, the current through the conductor increases proportionally.

This statement is expressed in Ohm’s law,
V = IR


where V is the voltage, I is the current, and R is the proportionality constant called the resistance.

WHAT IS CAPACITANCE? BASIC INFORMATION AND TUTORIALS

Capacitance (C) is the phenomenon whereby a circuit stores electrical energy. Whenever two conducting materials are separated by an insulating material, they have the ability of storing electrical energy.

Such an arrangement of materials (two conductors separated by an insulator) is called a capacitor or condenser. If a source of dc voltage is connected between the two conducting materials of a capacitor, a current will flow for a certain length of time.

The current initially will be relatively large but will rapidly diminish to zero. A certain amount of electrical energy will then be stored in the capacitor.

If the source of voltage is removed and the conductors of the capacitor are connected to the two ends of a resistor, a current will flow from the capacitor through the resistor for a certain length of time. The current initially will be relatively large but will rapidly diminish to zero.

The direction of the current will be opposite to the direction of the current when the capacitor was being charged by the dc source. When the current reaches zero, the capacitor will have dissipated the energy which was stored in it as heat energy in the resistor. The capacitor will then said to be discharged.

The two conducting materials, often called the plates of the capacitor, will be electrically charged when electrical energy is stored in the capacitor. One plate will have an excess of positive electricity and therefore will be positively charged with a certain number of coulombs of excess positive electricity.

The other plate will have an excess of negative electricity and therefore will be negatively charged with an equal number of coulombs of excess negative electricity. When in this state, the capacitor is said to be charged. When a capacitor is charged, a voltage is present between the two conductors, or plates, of the capacitor.

When a capacitor is in a discharged state, no electrical energy is stored in it, and there is no potential difference, no voltage, between its plates. Each plate contains just as much positive as negative electricity, and neither plate has any electric charge.

From the above discussion it is seen that a capacitor has a sustained current only as long as the voltage is changing. A capacitor connected to a dc supply will not have a sustained current. In an ac circuit, the voltage is continually changing from instant to instant.

Therefore, when a capacitor is connected to an ac supply, an alternating current continues to flow. The current is first in one direction, charging the capacitor, and then in the opposite direction, discharging the capacitor.

Farad (F) The unit of capacitance. It is designated by the symbol F. A circuit or capacitor will have a capacitance of 1 F if when the voltage across it is increased by 1 V, its stored electricity is increased by 1 C.

Another definition for a capacitance of 1 F, which results in the same effect, is given below. A circuit or capacitor will have a capacitance of 1 F when if the voltage impressed upon it is changed at the rate of 1 V/s, 1 A of charging current flows.

Capacitive reactance (Xc) is the name given to the opposition to the flow of alternating current due to capacitance. It is measured in ohms as resistance and inductive reactance are.

CIRCUIT ANALYSIS TYPE BASIC INFORMATION

Circuit Reduction Techniques.

When a circuit analyst wishes to find the current through or the voltage across one of the elements that make up a circuit, as opposed to a complete analysis, it is often desirable to systematically replace elements in a way that leaves the target elements unchanged, but simplifies the remainder in a variety of ways.

The most common techniques include series/parallel combinations, wye/delta (or tee/pi) combinations, and the Thevenin-Norton theorem.

Series Elements.

Two or more electrical elements that carry the same current are defined as being in series.

Parallel Elements.

Two or more electrical elements that are connected across the same voltage are defined as being in parallel.

Wye-Delta Connections.

A set of three elements may be connected either as a wye, shown in or a delta. These are also called tee and pi connections, respectively. The equations give equivalents, in terms of resistors, for converting between these connection forms.

Thevenin-Norton Theorem.

The Thevenin theorem and its dual, the Norton theorem, provide the engineer with a convenient way of characterizing a network at a terminal pair. The method is most useful when one is considering various loads connected to a pair of output terminals. The equivalent can be determined analytically, and in some cases, experimentally.

Thevenin Theorem.

This theorem states that at a terminal pair, any linear network can be replaced by a voltage source in series with a resistance (or impedance). It is possible to show that the voltage is equal to the voltage at the terminal pair when the external load is removed (open circuited), and that the resistance is equal to the resistance calculated or measured at the terminal pair with all independent sources de-energized. 

De-energization of an independent source means that the source voltage or current is set to zero but that the source resistance (impedance) is unchanged. Controlled (or dependent) sources are not changed or de-energized.

Norton Theorem.

This theorem states that at a terminal pair, any linear network can be replaced by a current source in parallel with a resistance (or impedance). It is possible to show that the current is equal to the current that flows through the short-circuited, terminal pair when the external load is short circuited, and that the resistance is equal to the resistance calculated or measured at the terminal pair with all independent sources de-energized. 

De-energization of an independent source means that the source voltage or current is set to zero but that the source resistance (impedance) is unchanged. Controlled (or dependent) sources are not changed or de-energized.

MAGNETIC PROPERTIES AND APPLICATIONS BASIC INFORMATION AND TUTORIALS

The relative importance of the various magnetic properties of a magnetic material varies from one application to another. In general, properties of interest may include normal induction, hysteresis, dc permeability, ac permeability, core loss, and exciting power.

It should be noted that there are various means of expressing ac permeability. The choice depends primarily on the ultimate use. Techniques for the magnetic testing of many magnetic materials are described in the ASTM standards.

The magnetic and electric circuits employed in magnetic testing of a specimen are as free as possible from any unfavorable design factors which would prevent the measured magnetic data from being representative of the inherent magnetic properties of the specimen.

The flux “direction” in the specimen is normally specified, since most magnetic materials are magnetically anisotropic. In most ac magnetic tests, the waveform of the flux is required to be sinusoidal.

As a result of the existence of unfavorable conditions, such as those listed and described below, the performance of a magnetic material in a magnetic device can be greatly deteriorated from that which would be expected from magnetic testing of the material.

Allowances for these conditions, if present, must be made during the design of the device if the performance of the device is to be correctly predicted.

Leakage.

A principal difficulty in the design of many magnetic circuits is due to the lack of a practicable material which will act as an insulator with respect to magnetic flux. This results in magnetic flux seldom being completely confined to the desired magnetic circuit. Estimates of leakage flux for a particular design may be made based on experience and/or experimentation.

Flux Direction.

Some magnetic materials have a very pronounced directionality in their magnetic properties. Failure to utilize these materials in their preferred directions results in impaired magnetic properties.

Fabrication.

Stresses introduced into magnetic materials by the various fabricating techniques often adversely affect the magnetic properties of the materials. This occurs particularly in materials having high permeability. Stresses may be eliminated by a suitable stress-relief anneal after fabrication of the material to final shape.

Joints.

Joints in an electromagnetic core may cause a large increase in total excitation requirements. In some cores operated on ac, core loss may also be increased.

Waveform.

When a sinusoidal voltage is applied to an electromagnetic core, the resulting magnetic flux is not necessarily sinusoidal in waveform, especially at high inductions. Any harmonics in the flux waveform cause increases in core loss and required excitation power.

Flux Distribution.

If the maximum and minimum lengths of the magnetic path in an electromagnetic core differ too much, the flux density may be appreciably greater at the inside of the core structure than at the outside. For cores operated on ac, this can cause the waveform of the flux at the extremes of the core structure to be distorted even when the total flux waveform is sinusoidal.

MAGNET WIRE INSULATION BASICS AND TUTORIALS

What are magnet wire insulations?

The term magnet wire includes an extremely broad range of sizes of both round and rectangular conductors used in electrical apparatus. Common round-wire sizes for copper are AWG No. 42 (0.0025 in) to AWG No. 8 (0.1285 in).

A significant volume of aluminum magnet wire is produced in the size range of AWG No. 4 to AWG No. 26. Ultrafine sizes of round wire, used in very small devices, range as low as AWG No. 60 for copper and AWG No. 52 for aluminum.

Approximately 20 different “enamels” are used commercially at present in insulating magnet wire.

Magnet wire insulations are high in electrical, physical, and thermal performance and best in space factor. The most widely used polymers for film-insulated magnet wire are based on polyvinyl acetals, polyesters, polyamideimides, polyimides, polyamides, and polyurethanes.

Many magnet wire constructions use different layers of these polymer types to achieve the best combination of properties. The most commonly used magnet wire is NEMA MW-35C, Class 200,\ which is constructed with a polyester basecoat and a polyamideimide topcoat.

Polyurethanes are employed where ease of solderability without solvent or mechanical striping is required. The thermal class of polyurethane insulations has been increased up to Class 155 and even Class 180.

Magnet wire products also are produced with fabric layers (fiberglass or Dacron-fiberglass) served over bare or conventional film-insulated magnet wire. Self-bonding magnet wire is produced with a thermoplastic cement as the outer layer, which can be heat-activated to bond the wires together.

DIELECTRIC STRENGTH DEFINITION AND BASIC INFORMATION TUTORIALS

What is dielectric strength?

Dielectric Strength is defined by the ASA as the maximum potential gradient that the material can withstand without rupture. Practically, the strength is often reported as the breakdown voltage divided by the thickness between electrodes, regardless of electrode stress concentration.

Breakdown appears to require not only sufficient electric stress but also a certain minimum amount of energy. It is a property which varies with many factors such as thickness of the specimen, size and shape of electrodes used in applying stress, form or distribution of the field of electric stress in the material, frequency of the applied voltage, rate and duration of voltage application, fatigue with repeated voltage applications, temperature, moisture content, and possible chemical changes under stress.

The practical dielectric strength is decreased by defects in the material, such as cracks, and included conducting particles and gas cavities. As will be shown in more detail in later sections on gases and liquids, the dielectric strength is quite adversely affected by conducting particles.

To state the dielectric strength correctly, the size and shape of specimen, method of test, temperature, manner of applying voltage, and other attendant conditions should be particularized as definitely as possible.

ASTM standard methods of dielectric strength testing should be used for making comparison tests of materials, but the levels of dielectric strength measured in such tests should not be expected to apply in service for long times. It is best to test an insulation in the same configuration in which it would be used.

Also, the possible decline in dielectric strength during long-time exposure to the service environment, thermal aging, and partial discharges (corona), if they exist at the applied service voltage, should be considered. ASTM has thermal life test methods for assessing the long-time endurance of some forms of insulation such as sheet insulation, wire enamel, and others.

There are IEEE thermal life tests for some systems such as random wound motor coils. The dielectric strength varies as the time and manner of voltage application.

With unidirectional pulses of voltage, having rise times of less than a few microseconds, there is a time lag of breakdown, which results in an apparent higher strength for very short pulses. In testing sheet insulation in mineral oil, usually a higher strength for pulses of slow rise time and somewhat higher strength for dc voltages is observed.

The trend in breakdown voltage with time is typical of many solid insulation systems. With ac voltages, the apparent strength declines steadily with time as a result of partial discharges (in the ambient medium at the conductor or electrode edge). These penetrate the solid insulation.

The discharges result from breakdown of the gas or liquid prior to the breakdown of the solid. Mica in particular, as well as other inorganic materials, is more resistant to such discharges. Organic resins should be used with caution where the ac voltage gradient is high and partial discharges (corona) may be present.

Since the presence of partial discharges on insulation is so important to the longtime voltage endurance, their detection and measurement have become very important quality control and design tools. 

If discharges continuously strike the insulation within internal cavities or on the surface, the time to failure usually varies inversely as the applied frequency, since the number of discharges per unit time increases almost in direct proportion to the frequency. But in some cases, ambient conditions prevent continuous discharges.

AWG (AMERICAN WIRE GAGE) CONDUCTOR SIZE DESIGNATION BASIC AND TUTORIALS

What is the American wire gage?

American wire gage, also known as the Brown & Sharpe gage, was devised in 1857 by J. R. Brown. It is usually abbreviated AWG.

This gage has the property, in common with a number of other gages, that its sizes represent approximately the successive steps in the process of wire drawing.

Also, like many other gages, its numbers are retrogressive, a larger number denoting a smaller wire, corresponding to the operations of drawing. These gage numbers are not arbitrarily chosen, as in many gages, but follow the mathematical law upon which the gage is founded.

Basis of the AWG is a simple mathematical law. The gage is formed by the specification of two diameters and the law that a given number of intermediate diameters are formed by geometric progression.

Thus, the diameter of No. 0000 is defined as 0.4600 in and of No. 36 as 0.0050 in. There are 38 sizes between these two; hence the ratio of any diameter to the diameter of the next greater number is given by this expression

The square of this ratio = 1.2610. The sixth power of the ratio, that is, the ratio of any diameter to the diameter of the sixth greater number, = 2.0050. The fact that this ratio is so nearly 2 is the basis of numerous useful relations or shortcuts in wire computations.

There are a number of approximate rules applicable to the AWG which are useful to remember:

1. An increase of three gage numbers (e.g., from No. 10 to 7) doubles the area and weight and consequently halves the dc resistance.

2. An increase of six gage numbers (e.g., from No. 10 to 4) doubles the diameter.

3. An increase of 10 gage numbers (e.g., from No. 10 to 1/0) multiplies the area and weight by 10 and divides the resistance by 10.

4. A No. 10 wire has a diameter of about 0.10 in, an area of about 10,000 cmils, and (for standard annealed copper at 20°C) a resistance of approximately 1.0 #/1000 ft.

5. The weight of No. 2 copper wire is very close to 200 lb/1000 ft (90 kg/304.8 m).

DIELECTRIC LOSS AND CORONA BASIC INFORMATION AND TUTORIALS

Dielectric Hysteresis and Conductance

When an alternating voltage is applied to the terminals of a capacitor, the dielectric is subjected to periodic stresses and displacements. If the material were perfectly elastic, no energy would be lost during any cycle, because the energy stored during the periods of increased voltage would be given up to the circuit when the voltage is decreased.

However, since the electric elasticity of dielectrics is not perfect, the applied voltage has to overcome molecular friction or viscosity, in addition to the elastic forces. The work done against friction is converted into heat and is lost. This phenomenon resembles magnetic hysteresis in some respects but differs in others.

It has commonly been called dielectric hysteresis but is now often called dielectric loss. The energy lost per cycle is proportional to the square of the applied voltage.

An imperfect capacitor does not return on discharge the full amount of energy put into it. Sometime after the discharge, an additional discharge may be obtained. This phenomenon is known as dielectric absorption.

A capacitor that shows such a loss of power can be replaced for purposes of calculation by a perfect capacitor with an ohmic conductance shunted around it. This conductance (or “leakance”) is of such value that its PR loss is equal to the loss of power from all causes in the imperfect capacitor.

The actual current through the capacitor is then considered as consisting of two components—the leading reactive component through the ideal capacitor and the loss component, in phase with the voltage, through the shunted conductance.

Electrostatic Corona.

When the electrostatic flux density in the air exceeds a certain value, a discharge of pale violet color appears near the adjacent metal surfaces. This discharge is called electrostatic corona.

In the regions where the corona appears, the air is electrically ionized and is a conductor of electricity. When the voltage is raised further, a brush discharge takes place, until the whole thickness of the dielectric is broken down and a disruptive discharge, or spark, jumps from one electrode to the other.

Corona involves power loss, which may be serious in some cases, as on transmission lines. Corona can form at sharp corners of high-voltage switches, bus bars, etc., so the radii of such parts are made large enough to prevent this.

A voltage of 12 to 25 kV between conductors separated by a fraction of an inch, as between the winding and core of a generator or between sections of the winding of an air-blast transformer, can produce a voltage gradient sufficient to cause corona.

A voltage of 100 to 200 kV may be required to produce corona on transmission-line conductors that are separated by several feet. Corona can have an injurious effect on fibrous insulation.

SKIN EFFECT – BASIC DEFINITION AND TUTORIALS

What is skin effect?

Real, or ohmic, resistance is the resistance offered by the conductor to the passage of electricity. Although the specific resistance is the same for either alternating or continuous current, the total resistance of a wire is greater for alternating than for continuous current.

This is due to the fact that there are induced emfs in a conductor in which there is alternating flux. These emfs are greater at the center than at the circumference, so the potential difference tends to establish currents that oppose the current at the center and assist it at the circumference.

The current is thus forced to the outside of the conductor, reducing the effective area of the conductor. This phenomenon is called skin effect.

Skin-Effect Resistance Ratio. The ratio of the A.C. resistance to the D.C. resistance is a function of the cross-sectional shape of the conductor and its magnetic and electrical properties as well as of the frequency.

For cylindrical cross sections with presumed constant values of relative permeability and resistivity, the function that determines the skin-effect ratio is

where r is the radius of the conductor and f is the frequency of the alternating current. The ratio of R, the A.C. resistance, to R0, the D.C. Resistance.

Skin Effect On Steel Wires and Cables.

The skin effect of steel wires and cables cannot be calculated accurately by assuming a constant value of the permeability, which varies throughout a large range during every cycle. Therefore, curves of measured characteristics should be used. See Electrical Transmission and Distribution Reference Book, 4th ed., 1950.

Skin Effect of Tubular Conductors.

Cables of large size are often made so as to be, in effect, round, tubular conductors. Their effective resistance due to skin effect may be taken from the curves of Sec. 4. The skin-effect ratio of square, tubular bus bars may be obtained from semiempirical formulas in the paper “A-C Resistance of Hollow, Square Conductors,” by A. H. M. Arnold, J. IEE (London), 1938, vol. 82, p. 537.

These formulas have been compared with tests. The resistance ratio of square tubes is somewhat larger than that of round tubes. Values may be read from the curves of Fig. 4, Chap. 25, of Electrical Coils and Conductors.

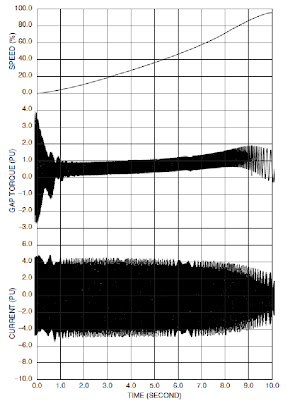
SYNCHRONOUS MOTOR AND CONDENSER STARTING BASIC INFORMATION AND TUTORIALS

The duty on self-starting synchronous motors and condensors is severe, as there are large induction currents in the starting cage winding once the stator winding is energized (see Fig. 5.6).

FIGURE 5.6 Synchronous motor and condensor starting.

These persist as the motor comes up to speed, similar to but not identical to starting an induction motor. Similarities exist to the extent that extremely high torque impacts the rotor initially and decays rapidly to an average value, increasing with time.

Different from the induction motor is the presence of a large oscillating torque. The oscillating torque decreases in frequency as the rotor speed increases.

This oscillating frequency is caused by the saliency effect of the protruding poles on the rotor.

Meanwhile, the stator current remains constant until 80% speed is reached. The oscillating torque at decaying frequency may excite train torsional natural frequencies during acceleration, a serious train design consideration.

An anomaly occurs at half speed as a dip in torque and current due to the coincidence of line frequency torque with oscillating torque frequency. Once the rotor is close to rated speed, excitation is applied to the field coils and the rotor pulls into synchronism with the rotating electromagnetic poles.

At this point, stable steady-state operation begins.

Increasingly, variable frequency power is supplied to synchronous machinery primarily to deliver the optimum motor speed to meet load requirements, improving the process efficiency. It can also be used for soft-starting the synchronous motor or condenser.

Special design and control are employed to avert problems imposed, such as excitation of train torsional natural frequencies and extra heating from harmonics of the supply power.

DIFFERENT TYPES OF MAGNETIC MATERIALS BASIC INFORMATION AND TUTORIALS

All materials have magnetic properties. These characteristic properties may be divided into five groups as follows:

● diamagnetic

● paramagnetic

● ferromagnetic

● antiferromagnetic

● ferrimagnetic

Only ferromagnetic and ferrimagnetic materials have properties which are useful in practical applications. Ferromagnetic properties are confined almost entirely to iron, nickel and cobalt and their alloys. The only exceptions are some alloys of manganese and some of the rare earth elements.

Ferrimagnetism is the magnetism of the mixed oxides of the ferromagnetic elements. These are variously called ferrites and garnets. The basic ferrite is magnetite, or Fe3O4, which can be written as FeO.Fe2O3. By substituting the FeO with other divalent oxides, a wide range of compounds with useful properties can be produced.

The main advantage of these materials is that they have high electrical resistivity which minimizes eddy currents when they are used at high frequencies. The important parameters in magnetic materials can be defined as follows:

● permeability – this is the flux density B per unit of magnetic field H. It is usual and more convenient to quote the value of relative permeability μr, which is B/μoH. A curve showing the variation of permeability with magnetic field for a ferromagnetic material is given in Fig. 3.1.

This is derived from the initial magnetization curve and it indicates that the permeability is a variable which is dependent on the magnetic field. The two important values are the initial permeability, which is the slope of the magnetization curve at H = 0, and the maximum permeability, corresponding to the knee of the magnetization curve.

● saturation – when sufficient field is applied to a magnetic material it becomes saturated. Any further increase in the field will not increase the magnetization and any increase in the flux density will be due to the added field. The saturation magnetization is Ms in amperes per metre and Js or Bs in tesla.

● remanence, Br and coercivity, Hc – these are the points on the hysteresis loop shown in Fig. 3.2 at which the field H is zero and the flux density B is zero, respectively. It is assumed that in passing round this loop, the material has been saturated. If this is not the case, an inner loop is traversed with lower values of remanence and coercivity.

Ferromagnetic and ferrimagnetic materials have moderate to high permeabilities. The permeability varies with the applied magnetic field, rising to a maximum at the knee of the B–H curve and reducing to a low value at very high fields.

These materials also exhibit magnetic hysteresis, where the intensity of magnetization of the material varies according to whether the field is being increased in a positive sense or decreased in a negative sense, as shown in Fig. 3.2.

When the magnetization is cycled continuously around a hysteresis loop, as for example when the applied field arises from an alternating current, there is an energy loss proportional to the area of the included loop.

This is the hysteresis loss, and it is measured in joules per cubic metre. High hysteresis loss is associated with permanent magnetic characteristics exhibited by materials commonly termed hard magnetic materials, as these often have hard mechanical properties.

Those materials with low hysteresis loss are termed soft and are difficult to magnetize permanently. Ferromagnetic or ferrimagnetic properties disappear reversibly if the material is heated above the Curie temperature, at which point it becomes paramagnetic, that is effectively non-magnetic.

ENERGY TRANSFORMATION EFFECTS BASIC INFORMATION AND TUTORIALS

Most electrical energy is generated by electromagnetic induction. However, electricity can be produced by other means. Batteries use electrochemistry to produce low voltages.

An electrolyte is a solution of chemicals in water such that the chemical separates into positively and negatively charged ions when dissolved. The charged ions react with the conducting electrodes and release energy, as well as give up their charge

A fixed electrode potential is associated with the reaction at each electrode; the difference between the two electrode potentials drives a current around an external circuit. The electrolyte must be sealed into a safe container to make a suitable battery.

‘Dry’ cells use an electrolyte in the form of a gel or thick paste. A primary cell releases electricity as the chemicals react, and the cell is discarded once all the active chemicals have been used up, or the electrodes have become contaminated. A secondary cell uses a reversible chemical reaction, so that it can be recharged to regenerate the active chemicals.

The fuel cell is a primary cell which is constructed so that the active chemicals (fuel) pass through the cell, and the cell can be used for long periods by replenishing the chemicals. Large batteries consist of cells connected in series or parallel to increase the output voltage or current.

Electricity can be generated directly from heat. When two different materials are used in an electrical circuit, a small electrochemical voltage (contact potential) is generated at the junction. In most circuits these contact potentials cancel out around the circuit and no current flows.

However, the junction potential varies with temperature, so that if one junction is at a different temperature from the others, the contact potentials will not cancel out and the net circuit voltage causes current to flow (Seebeck effect). The available voltage is very small, but can be made more useful by connecting many pairs of hot and cold junctions in series.

The thermocouple is used mostly for measurement of temperature by this effect, rather than for the generation of electrical power. The efficiency of energy conversion is greater with semiconductor junctions, but metal junctions have a more consistent coefficient and are preferred for accurate measurements.

The effect can be reversed with suitable materials, so that passing an electric current around the circuit makes one junction hotter and the other colder (Peltier effect). Such miniature heat pumps are used for cooling small components.

Certain crystalline chemicals are made from charged ions of different sizes. When a voltage is applied across the crystal, the charged ions move slightly towards the side of opposite polarity, causing a small distortion of the crystal. Conversely, applying a force so as to distort the crystal moves the charged ions and generates a voltage.

This piezoelectric effect is used to generate high voltages from a small mechanical force, but very little current is available. Ferromagnetic materials also distort slightly in a magnetic field. The magnetostrictive effect produces low frequency vibration (hum) in ac machines and transformers.

Electricity can be produced directly from light. The photovoltaic effect occurs when light falls on suitable materials, releasing electrons from the material and generating electricity. The magnitude of the effect is greater with short wavelength light (blue) than long wavelength light (red), and stops altogether beyond a wavelength threshold.

Light falling on small photovoltaic cells is used for light measurement, communications and for proximity sensors. On a larger scale, semiconductor solar cells are being made with usable efficiency for power generation.

Light is produced from electricity in incandescent filament bulbs, by heating a wire to a sufficiently high temperature that it glows. Fluorescent lights produce an electrical discharge through a low pressure gas. The discharge emits ultraviolet radiation, which causes a fluorescent coating on the inside of the tube to glow.

TURBINE GENERATOR STANDARD AND OPTIONAL EQUIPMENT

Standard Equipment

The manufacturer shall equip the turbine-generator unit with the following standard equipment:

1) Speed/Load-Control System.

A speed /load-control system capable of controlling and regulating the speed of the turbine in conformity with the performance characteristics hereinafter specified. The speed/load-control system should include means by which the steady-state speed regulation may be adjusted to values within the limits hereinafter specified.

Adjustment of the steady-state speed regulation, while the turbine is in operation, is not required by this recommended practice unless otherwise agreed upon between the manufacturer and the purchaser.

2) Speed/Load Reference Changer.

A speed/load changer by means of which the speed or power output of the turbine may be changed within the limits hereinafter specified while the turbine is in operation. The speed/load reference changer shall be equipped with means for manual adjustment and should be equipped to accept input(s) for remote control.

3) Valve Position Limiter (Load Limit).

For turbines rated over 10 MW, a valve position limiter manually adjustable to limit the degree of opening of the control valves to any value within the full range of valve travel while the turbine is in operation.

If this device is used for load-limiting purposes, the speed-control system will not necessarily control the overspeed of the turbine, if the speed/load reference changer is set at its high-speed stop.

4) Miscellaneous.

At the discretion of the manufacturer, any instruments, controls, or safety devices not specified as standard equipment in (1), (2), and (3) may be included.

Optional Equipment

The following devices or other optional devices may be specified by the purchaser:

1) Valve Position Limiter.

For turbines rated 10 MW or under, a valve position limiter.

2) Adjustment of Steady-State Regulation.

A means by which, in the speed/load-control system the steady-state speed regulation may be adjusted, within limits agreed to by the manufacturer and purchaser, while the turbine is operating at any power output.

3) Remote or Local Indication.

A means for remote or local indication, or both, of the positions of the control valves or any other element of the control system to be specified by the purchaser.

4) Remote Control of the Valve Position Limiter.

For turbines rated over 10 MW, a means for remote setting of the valve position limiter within the limits hereinafter specified.

5) Remote Control of Speed/Load Reference Changer.

For turbines rated over 10 MW, a means for remote control of the speed/load reference changer within the limits hereinafter specified.

6) Miscellaneous.

At the discretion of the manufacturer, any instruments, controls, or safety devices not previously specified as optional equipment may be included.

WHAT ARE ELECTROMAGNETS – DEFINITION BASICS AND TUTORIALS

It was noted previously in this section that an electric current flowing through a conductor creates a magnetic field around the conductor. In Fig. 2.9, the shaded circle represents a cross section of a

conductor with current flowing in toward the paper. The current is flowing from negative to positive.

When the current flows as indicated, the magnetic field is in a counterclockwise direction. This is easily determined by the use of the left-hand rule, which is based upon the true direction of current flow. When a wire is grasped in the left hand with the thumb pointing from negative to positive, the magnetic field around the conductor is in the direction that the fingers are pointing.

If a current-carrying wire is bent into a loop, the loop assumes the properties of a magnet; that is, one side of the loop will be a north pole and the other side will be a south pole. If a soft-iron core is placed in the loop, the magnetic lines of force will traverse the iron core and it becomes a magnet.

When a wire is made into a coil and connected to a source of power, the fields of the separate turns join and thread through the entire coil as shown in Fig. 2.10a. Figure 2.10b shows a cross section of the same coil. Note that the lines of force produced by one turn of the coil combine with the lines of force from the other turns and thread through the coil, thus giving the coil a magnetic polarity.

The polarity of the coil is easily determined by the use of the left-hand rule for coils: When a coil is grasped m the left hand with the fingers pointing in the direction of current flow, that is, from negative to positive, the thumb will point toward the north pole of the coil.

When a soft-iron core is placed in a coil, an electromagnet is produced. Of course, the wire in the coil must be insulated so that there can be no short circuit between the turns of the coil. A typical electromagnet is made by winding many turns of insulated wire on a soft-iron core which has been wrapped with an insulating material.

The turns of wire are placed as close together as possible to help prevent magnetic lines of force from passing between the turns. Figure 2.11 is a cross-sectional drawing of an electromagnet. The strength of an electromagnet is proportional to the product of the current passing through the coil and the number of turns in the coil.

This value is usually expressed in ampere-turns. If a current of 5 amp is flowing in a coil of an electromagnet and there are 300 turns of wire in the coil, the coil will have an mmf of 1,500 amp-turns. Since the gilbert is also a measure of mmf and 1 amp-turn is equal to 1.26 gilberts, the mmf may also be given as 1,890 gilberts.  The ultimate strength of the magnet also depends upon the permeability of the core material.

The force exerted upon a magnetic material by an electromagnet is inversely proportional to the square of the distance between the pole of the magnet and the material. For example, if a magnet exerts a pull of 1 Ib upon an iron bar when the bar is f in. from the magnet, then the pull will only be & lb when the bar is 1 in. from the magnet.

For this reason, the design of electrical equipment using electromagnetic actuation requires careful consideration of the distance through which the magnetic force must act. This is especially important in voltage regulators and relays.

WHAT IS FARADAY'S LAW OF ELECTROMAGNETIC INDUCTION – DEFINITION AND BASIC TUTORIALS

The famous author Isaac Asimov once said, “The most exciting phrase to hear in science, the one that heralds new discoveries, is not ‘Eureka!’ (I found it!) but, ‘That’s funny. …’ ” That might have been what Faraday thought when he noticed the meter deflection upon connecting and disconnecting the battery.

According to Faraday’s law, in any closed linear path in space, when the magnetic flux #  surrounded by the path varies with time, a voltage is induced around the path equal to the negative rate of change of the flux in webers per second.

V = dp/dt

The minus sign denotes that the direction of the induced voltage is such as to produce a current opposing the flux. If the flux is changing at a constant rate, the voltage is numerically equal to the increase or decrease in webers in 1 s.

The closed linear path (or circuit) is the boundary of a surface and is a geometric line having length but infinitesimal thickness and not having branches in parallel.

It can vary in shape or position. If a loop of wire of negligible cross section occupies the same place and has the same motion as the path just considered, the voltage will tend to drive a current of electricity around the wire, and this voltage can be measured by a galvanometer or voltmeter connected in the loop of wire.

As with the path, the loop of wire is not to have branches in parallel; if it has, the problem of calculating the voltage shown by an instrument is more complicated and involves the resistances of the branches.

Even though he didn’t get the result he was looking for in his earlier experiment— current flowing steadily through the secondary coil — he did see a hint of current flow in the form of a slight needle deflection in the galvanometer.

But it was enough to lead him down the right path to the answer. Eventually, he found that a stationary magnetic field does not induce current in the secondary coil, but that a changing magnetic field does.

When a battery is first connected to a circuit, the magnetic field has to build from zero to its maximum. As the field grows, the lines of flux of the magnetic field cut the turns of wire in the secondary coil, thereby inducing a current.

Faraday deduced that a changing magnetic field whose lines of flux cut through a wire will generate a voltage. The value of the voltage is proportional to the rate of change and the intensity of the magnetic flux. This is known as Faraday’s law of induction.

According to Faraday’s law of induction, it doesn’t matter whether the lines of flux are cutting through the wire or the wire is moving through the lines of flux, as long as they are moving relative to each other. Therefore, a wire can move through a stationary magnetic field or a magnetic field can move through a stationary wire and it will still generate voltage.

What is important is that the wire is not moving parallel relative to the lines of flux (0°), otherwise no lines of flux will be cut and no voltage will be generated. The movement can, however, be somewhere in between parallel and perpendicular (90°) relative to each other; then some lines of flux will be cut and a proportional amount of voltage will be generated.

For example, if a wire is moving at a 60° angle through a magnetic field, then it is cutting half as many lines of flux as another wire traveling at a 90° angle to the magnetic field at the same rate of speed. Therefore, it would generate half the voltage.

KIRCHHOFF'S CURRENT LAW BASIC INFORMATION AND TUTORIALS

Kirchhoff’s current law (KCL) states that the currents entering and leaving any branch point or node in the circuit must add up to zero.

This follows directly from the conservation property: electric charge is neither created nor destroyed, nor is it “stored” (in appreciable quantity) within our wires, so that all the charge that flows into any junction must also flow out.

Thus, if three wires connect at one point, and we know the current in two of them, they determine the current in the third.

Again, the analogy of flowing water helps make this more obvious. At a point where three pipes are connected, the amount of water flowing in must equal the amount flowing out (unless there is a leak). 

For the purpose of computation, we assign positive or negative signs to currents flowing in and out of the node, respectively.

It does not matter which way we call positive, as long as we remain consistent in our definition. Then, the sum of currents into (or out of) the node is zero.

This is illustrated with the simple example in Figure 2.5, where KCL applied to the branch point proves that the current through the battery equals the sum of currents through the individual resistors.

Despite their simple and intuitive nature, the fundamental importance of Kirchhoff’s laws cannot be overemphasized. They lie at the heart of the interdependence of the different parts and branches of power systems: whenever two points are electrically connected, their voltages and the currents through them must obey KVL and KCL, whether this is operationally and economically desirable or not.

For example, managing transmission constraints in power markets is complicated by the fact that the flow on any one line cannot be changed independently of others. Thus the engineer’s response to the economist’s lamentation of how hard it is to manage power transmission: “Blame Kirchhoff.”

KIRCHHOFF'S VOLTAGE LAW BASIC INFORMATION AND TUTORIALS

Kirchhoff’s voltage law (often abbreviated KVL) states that the sum of voltages around any closed loop in a circuit must be zero. In essence, this law expresses the basic properties that are inherent in the definition of the term “voltage” or “electric potential.”

Specifically, it means that we can definitively associate a potential with a particular point that does not depend on the path by which a charge might get there. 

This also implies that if there are three points (A, B, and C) and we know the potential differences between two pairings (between A and B and between B and C), this determines the third relationship (between A and C).

Without thinking in such abstract and general terms, we apply this principle when we move from one point to another along a circuit by adding the potential differences or voltages along the way, so as to express the cumulative voltage between the initial and final point.

Finally, when we go all the way around a closed loop, the initial and final point are the same, and therefore must be at the same potential: a zero difference in all.

The analogy of flowing water comes in handy. Here, the voltage at any given point corresponds to the elevation. A closed loop of an electric circuit corresponds to a closed system like a water fountain. The voltage “rise” is a power source—say, a battery—that corresponds to the pump.

From the top of the fountain, the water then flows down, maybe from one ledge to another, losing elevation along the way and ending up again at the bottom. Analogously, the electric current flows “down” in voltage, maybe across several distinct steps or resistors, to finish at the “bottom” end of the battery.

This notion is illustrated by in the simple circuit in Figure 2.4 that includes one battery and two resistors. Note that it is irrelevant which point we choose to label as the “zero” potential: no matter what the starting point,adding all the potential gains and drops encountered throughout the complete loop will give a zero net gain.

WHAT IS RESISTANCE (CIRCUIT ANALYSIS) – DEFINITION BASICS AND TUTORIALS

To say that Ohm’s law is true for a particular conductor is to say that the resistance of this conductor is, in fact, constant with respect to current and voltage. Certain materials and electronic devices exhibit a nonlinear relationship between current and voltage, that is, their resistance varies depending on the voltage applied.

The relationship V = IR will still hold at any given time, but the value of R will be a different one for different values of V and I. These nonlinear devices have specialized applications and will not be discussed in this chapter.

Resistance also tends to vary with temperature, though a conductor can still obey Ohm’s law at any one temperature. For example, the resistance of a copper wire increases as it heats up. In most operating regimes, these variations are negligible.

Generally, in any situation where changes in resistance are significant, this is explicitly mentioned. Thus, whenever one encounters the term “resistance” without further elaboration, it is safe to assume that within the given context, this resistance is a fixed, unchanging property of the object in question.

Resistance depends on an object’s material composition as well as its shape. For a wire, resistance increases with length, and decreases with cross-sectional area. Again, the analogy to a gas or water pipe is handy: we know that a pipe will allow a higher flow rate for the same pressure difference if it has a greater diameter, while the flow rate will decrease with the length of the pipe.

This is due to friction in the pipe, and in fact, an analogous “friction” occurs when an electric current travels through a material.

This friction can be explained by referring to the microscopic movement of electrons or ions, and noting that they interact or collide with other particles in the material as they go. The resulting forces tend to impede the movement of the charge carriers and in effect limit the rate at which they pass.

These forces vary for different materials because of the different spatial arrangements of electrons and nuclei, and they determine the material’s ability to conduct. This intrinsic material property, independent of size or shape, is called resistivity and is denoted by r (the Greek lowercase rho).

The actual resistance of an object is given by the resistivity multiplied by the length of the object (l ) and divided by its cross-sectional area (A): R = RHO X LENGTH/ AREA

The units of resistance are ohms, (Greek capital omega). By rearranging Ohm’s law, we see that resistance equals voltage divided by current. Units of resistance are thus equivalent to units of voltage divided by units of current. By definition, one ohm equals one volt per ampere (OHM = V/A).

The units of resistivity are ohm-meters (OHM-m), which can be reconstructed through the preceding formula: when ohm-meters are multiplied by meters (for l ) and divided by square meters, the result is simply ohms.

Resistivity, which is an intrinsic property of a material, is not to be confused with the resistance per unit length (usually of a wire), quoted in units of ohms per meter (oHM/m). The latter measure already takes into account the wire diameter; it represents, in effect, the quantity rho/A. The resistivities of different materials in V-m can be found in engineering tables.

WHAT IS ELECTROMAGNETIC INDUCTION – DEFINITION BASICS AND TUTORIALS

Electric current creates a magnetic field, the reverse effect also exists: magnetic fields, in turn, can influence electric charges and cause electric currents to flow. However, there is an important twist: the magnetic field must be changing in order to have any effect.

A static magnetic field, such as a bar magnet, will not cause any motion of nearby charge. Yet if there is any relative motion between the charge and the magnetic field—for example, because either the magnet or the wire is being moved, or because the strength of the magnet itself is changing— then a force will be exerted on the charge, causing it to move.

This force is called an electromotive force (emf) which, just like an ordinary electric field, is distinguished by its property of accelerating electric charges. The most elementary case of the electromotive force involves a single charged particle traveling through a magnetic field, at a right angle to the field lines (the direction along which iron filings would line up).

This charge experiences a force again at right angles to both the field and its velocity, the direction of which (up or down) depends on the sign of the charge (positive or negative) and can be specified in terms of another right-hand rule, as illustrated in Figure 1.3.

This effect can be expressed concisely in mathematical terms of a cross product of vector quantities (i.e., quantities with a directionality in space, represented in boldface), in what is known as the Lorentz equation, F = ¼ qv X B where F denotes the force, q the particle’s charge, v its velocity, and B the magnetic field.

In the case where the angle between v and B is 908 (i.e., the charge travels at right angles to the direction of the field) the magnitude or numerical result for F is simply the arithmetic product of the three quantities. This is the maximum force possible: as the term cross product suggests, the charge has to move across the field in order to experience the effect.

The more v and B are at right angles to each other, the greater the force; the more closely aligned v and B are, the smaller the force. If v and B are parallel—that is, the charge is traveling along the magnetic field lines rather than across them—the force on the charge is zero. Figure 1.3 illustrates a typical application of this relationship.

The charges q reside inside a wire, being moved as a whole so that each of the microscopic charges inside has a velocity v in the direction of the wire’s motion. If we align our right hand with that direction v and then curl our fingers in the direction of the magnetic field B (shown in the illustration as pointing straight back into the page), our thumb will point in the direction of the force F on a positive test charge.

Because in practice the positive charges in a metal cannot move but the negatively charged electrons can, we observe a flow of electrons in the negative or opposite direction of F. 

Because only the relative motion between the charge and the magnetic field matters, the same effect results if the charge is stationary in space and the magnetic field is moved (e.g., by physically moving a bar magnet), or even if both the magnet and the wire are stationary but the magnetic field is somehow made to become stronger or weaker over time.

The phenomenon of electromagnetic induction occurs when this electromagnetic force acts on the electrons inside a wire, accelerating them in one direction along the wire and thus causing a current to flow. The current resulting from such a changing magnetic field is referred to as an induced current.

This is the fundamental process by which electricity is generated, which will be applied over and over within the many elaborate geometric arrangements of wires and magnetic fields inside actual generators.

WHAT IS AN ELECTRIC FIELD - DEFINITION BASICS AND TUTORIALS

We characterized the electric potential as a property of the location at which a charge might find itself. A map of the electric potential would indicate how much potential energy would be possessed by a charge located at any given point.

The electric field is a similar map, but rather of the electric force (such as attraction or repulsion) that would be experienced by that charge at any location.

This force is the result of potential differences between locations: the more dramatically the potential varies from one point to the next, the greater the force would be on an electric charge in between these points. In formal terms, the electric field represents the potential gradient.

Consider the electric field created by a single positive charge, just sitting in space. Another positive charge in its vicinity would experience a repulsive force. This repulsive force would increase as the two charges were positioned closer together, or decrease as they moved father apart; specifically, the electric force drops off at a rate proportional to the square of the distance.

This situation can be represented graphically by drawing straight arrows radially outward from the first charge, as in Figure 1.1a. Such arrows are referred to as field lines. Their direction indicates the direction that a “test charge,” such as the hypothetical second charge that was introduced, would be pushed or pulled (in this case, straight away).

The strength of the force is indicated by the proximity of field lines: the force is stronger where the lines are closer together. This field also indicates what would happen to a negative charge: At any point, it would experience a force of equal strength (assuming equal magnitude of charge), but opposite direction as the positive test charge, since it would be attracted rather than repelled.

Thus, a negative test charge would also move along the field lines, only backwards. By convention, the direction of the electric field lines is drawn so as to represent the movement of a positive test charge. For a slightly more complex situation, consider the electric field created by a positive and a negative charge, sitting at a fixed distance from each other.

We can map the field conceptually by asking, for any location, “What force would be acting on a (positive) test charge if it were placed here?” Each time, the net force on the test charge would be a combination of one attractive force and one repulsive force, in different directions and at different strengths depending on the distance from the respective fixed charges.

Graphically, we can construct an image of the field by drawing an arrow in the direction that the charge would be pulled. The arrows for points along the charge’s hypothetical path then combine into continuous field lines. Again, these field lines will be spaced more closely where the force is stronger. This exercise generates the picture in Figure 1.1b.